@Luukv93,
OK, this one took me a little while, but I think I cracked it. Buckle in - LONG post ahead while I try to explain what I did.
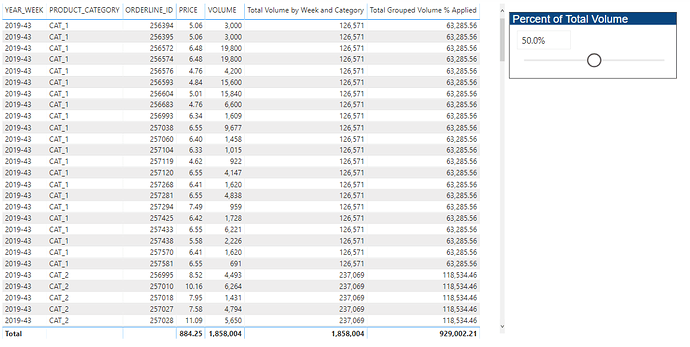
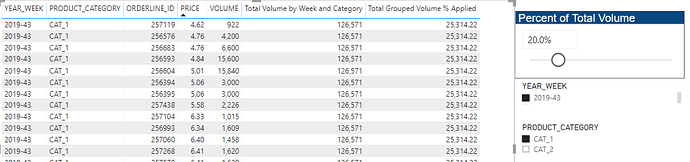
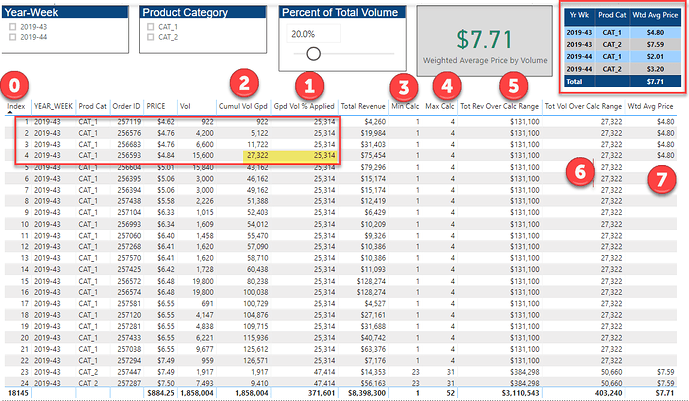
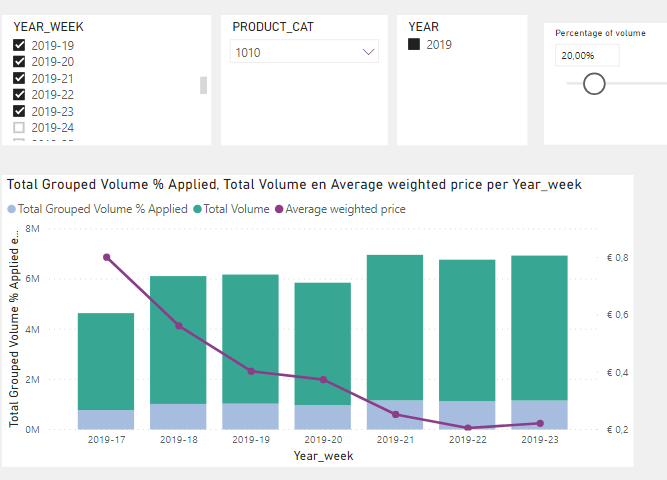
Here’s the solution table I’ll refer to in my explanation (full solution file posted at the bottom of this post):
Step 0: Power Query processing
- Sort Data table by YEAR_WEEK, Product Category, Order ID and Price - all ascending
- Add an index column, starting at 1 (this is perhaps the most critical step in the whole solution. For the calculations to work, you need to be able to filter and sum across specific row subsets. Usually this is done via a date field and date table, which we don’t have available here. But we can do the necessary cumulative totals and create the positional awareness using the index column instead)
- After doing this, create a calculated column for revenue equal to price times volume.
The Data table is now sufficiently prepped.
Measure 1: Total Grouped Volume % Applied
This is the measure we created above - sum of volume by year/week and product category multiplied by slicer percentage
Measure 2:
Cumulative Volume Grouped =
CALCULATE(
[Total Volume],
FILTER(
ALLEXCEPT(
Data,
Data[YEAR_WEEK],
Data[PRODUCT_CATEGORY]
),
Data[Index] <= MAX( Data[Index] )
)
)
This is the standard cumulative total pattern, just resetting for every change in year/week and product category.
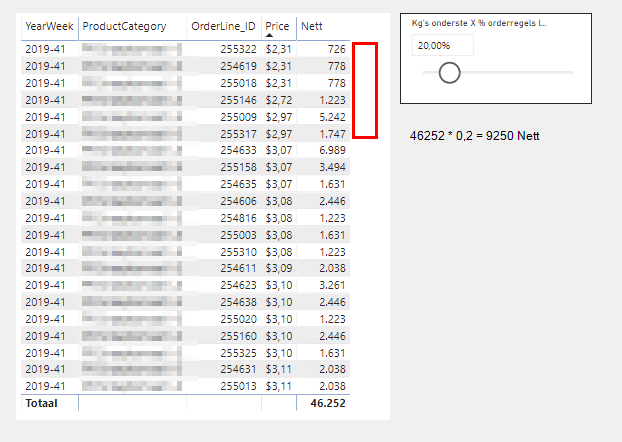
Now IMO the trickiest part of this whole solution is trying to characterize in DAX the red boundary in the screenshot, where measure 2 first exceeds measure 1 (highlighted in yellow), again resetting for every change in year/week and product category. I’m sure there are many other ways to do this, but here’s the approach I took:
Measure 3:
Min Calc Range Grouped =
CALCULATE(
MIN( Data[Index] ),
ALLEXCEPT(
Data,
Data[YEAR_WEEK],
Data[PRODUCT_CATEGORY]
)
)
This just calculates the minimum index of the calculation range (the red box), using the repeated ALLEXCEPT pattern.
Measure 4:
Max Calc Range Grouped =
CALCULATE(
MAX( Data[Index] ),
TOPN(
1,
FILTER(
ALLEXCEPT(
Data,
Data[YEAR_WEEK],
Data[PRODUCT_CATEGORY]),
[Cumulative Volume Grouped] > [Total Grouped Volume % Applied]
),
Data[Index],
ASC
),
ALLEXCEPT(
Data,
Data[YEAR_WEEK],
Data[PRODUCT_CATEGORY]
)
)
This is the measure the took me most time to figure out - it has a bit of everything – TOP N1, extensive use of the index for positional awareness, the repeated ALLEXCEPT, etc , but was the cornerstone for the remainder of the calculations, as you’ll see below.
Measure 5:
Total Revenue Over Calc Range =
SUMX(
FILTER(
ALLEXCEPT(
Data,
Data[YEAR_WEEK],
Data[PRODUCT_CATEGORY]
),
Data[Index] >= [Min Calc Range Grouped] &&
Data[Index] <= [Max Calc Range Grouped]
),
[Total Revenue]
)
This is the sum of P*Q (Total Revenue), filtered by the boundaries of the min and max range, defined by measures 3 and 4 above.
Measure 6:
Total Volume Over Calc Range
This is the exact same measure as above, just with volume instead of revenue.
Measure 7:
Weighted Average Price by Volume =
CALCULATE(
IF(
SELECTEDVALUE( Data[Index] ) <= [Max Calc Range Grouped],
DIVIDE(
[Total Revenue Over Calc Range],
[Total Volume Over Calc Range],
0
),
BLANK()
),
VALUES( Data[Index] )
)
This is the quotient of measures 5 and 6, which generates the volume -weighted average price calculated for the rows of the red box.
I’m sure there are more efficient ways of doing this, but I always find the measure branching approach extremely helpful in breaking down complex problems into manageable chunks. Hopefully, that’s a clear enough explanation to allow you to work through the solution file on your own.
Very interesting problem - I enjoyed working through this one with you. Hope this is helpful to you.
– Brian
eDNA Forum - Complex Ranking Cumulative Scenario - solution.pbix (61.6 KB)
P.S. - Your instincts in Post #1 were spot on (“The solution probably has to deal with a cumulative pattern and a TOPN/RANKX that resets for each YearWeek and ProductCategory.”). That’s exactly what I ended up doing, after a couple of interesting but ultimately unsuccessful detours…