Excel BI Challenge Workout 195

EnterpriseDNA · May 19, 2023, 11:41am

— CAN YOU SOLVE THIS - EXCEL CHALLENGE 195 —
(Solutions in any language are also welcome for Excel Challenges)

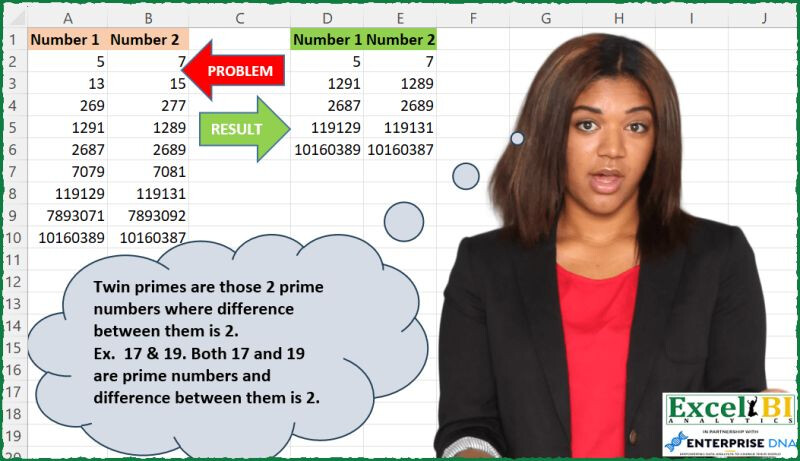
Twin primes are those 2 prime numbers where difference between them is 2.
Ex. 17 & 19. Both 17 and 19 are prime numbers and difference between them is 2.

Post answers in Comment.

(Your formula need not be a single formula. You can write multiple formulas to arrive at a solution. Also your formula need not be different from others as long as you have worked out your formula independently)

Download Practice File - https://lnkd.in/dnD_hc9y

#excel, #excelchallenge, #powerquerychallenge, #daxchallenge, #m, #dax, #powerbi, #powerquery, #powerpivot, #sheets, #googlesheets, #data, #analytics, #businessintelligence, #finance, #office365, #python, #r

Excel BI LinkedIn Post

EnterpriseDNA · May 19, 2023, 11:42am

LinkedIn post by
Bo Rydobon

M-Code

let
  Source = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],
  Ans = Table.SelectRows(Source, each let a = Record.ToList(_) , b = {2}&List.Select(List.Numbers(3,Int64.From(Number.Sqrt(List.Max(a)))/2,2),each _<List.Min(a))
    in if Number.Abs(a{0}-a{1})=2 then  List.AllTrue(List.Transform(a,(a)=> List.AllTrue(List.Transform(b,each Number.Mod(a,_)>0)))) else false )
in
  Ans

EnterpriseDNA · May 19, 2023, 11:44am

LinkedIn Post by:
JvdV

A bit verbose perhaps but thought it would be nice to (re-)create a function Excel is desperately missing:

=FILTER(A2:B10,MAP(A2:A10,B2:B10,LAMBDA(a,b,AND(ISPRIME(a),ISPRIME(b),ABS(a-b)=2))))

Where ISPRIME() is a named function:

=LAMBDA(x,SUM(N(MOD(x/SEQUENCE(SQRT(x)),1)=0))=1)

EnterpriseDNA · May 19, 2023, 11:44am

LinkedIn Post by:
محمد حلمي

=FILTER(A2:B10,BYROW(MAP(A2:B10,LAMBDA(a,LET(r,a/SEQUENCE(SQRT(a)),SUM(--(INT(r)=r))=1))),LAMBDA(a,SUM(-a)))+ABS(A2:A10-B2:B10)=0)

EnterpriseDNA · May 19, 2023, 11:45am

LinkedIn post by:
Alejandro Simón

Adjunto mi query…

Me encantó como lo manejó Omid Motamedisedeh . En base a eso mejoré el query utilizando Number.Mod para hacer más eficiente el cálculo.

let
Origen = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],
SelectRows = Table.SelectRows(Origen, each Number.Abs([Number 2]-[#"Number 1 "])=2),
Numero1 = List.Transform(SelectRows[#"Number 1 "], (x)=> List.Count([List.Select](http://list.select/)(List.Transform({1..x}, (y)=> Number.Mod(x,y)), each _ = 0))),
Numero2 = List.Transform(SelectRows[Number 2], (x)=> List.Count([List.Select](http://list.select/)(List.Transform({1..x}, (y)=> Number.Mod(x,y)), each _ = 0))),
Sol = Table.SelectRows(Table.FromColumns({SelectRows[#"Number 1 "], SelectRows[Number 2], Numero1, Numero2}, Table.ColumnNames(Origen)&{"Col3"}&{"Col4"}), each [Col3] = 2 and [Col4] = 2)[[#"Number 1 "], [Number 2]]
in
Sol

EnterpriseDNA · May 19, 2023, 11:46am

LinkedIn post by:
Sunny Baggu

=LET(
    _e1, LAMBDA(x, y, ABS(x - y) = 2),
    _e2, LAMBDA(v, OR(MOD(v, SEQUENCE(ROUNDUP(SQRT(v), 0) - 1, , 2)) = 0)),
    FILTER(
        A2:B10,
        MAP(
            A2:A10,
            B2:B10,
            LAMBDA(a, b,
                LET(
                    _cond1, _e1(a, b),
                    _cond2, NOT(OR(_e2(a), _e2(b))),
                    AND(_cond1, _cond2)
                )
            )
        )
    )
)

EnterpriseDNA · May 19, 2023, 11:47am

LinkedIn post by:
Pratik Sathe

To check if two numbers in Excel are twin primes, you can use the following formula:

=AND(ISNUMBER(A2), ISNUMBER(B2), ISPRIME(A2), ISPRIME(B2), ABS(A2-B2) =2)

Assuming that the first number is in cell A2, and the second number is in cell B2, this formula will return TRUE if both numbers are prime and the absolute difference between them is 2. Otherwise, it will return FALSE.

EnterpriseDNA · May 19, 2023, 11:48am

LinkedIn Post by:
Luan Rodrigues

let
  Fonte = Tabela1,
  fil = Table.SelectRows(Fonte, each ([#"Number 1 "] - [Number 2] = 2) or ([#"Number 1 "] - [Number 2] = -2)),
  add = Table.AddColumn(fil, "primo", each [
  a = Number.From([#"Number 1 "]),
  b = List.Count(List.Select(List.Transform(List.Buffer({1..a}), (x)=> a/x - Number.RoundDown(a/x)), each _ = 0)),
  a1 = Number.From([Number 2]),
  b1 = List.Count(List.Select(List.Transform(List.Buffer({1..a1}), (x)=> a1/x - Number.RoundDown(a1/x)), each _ = 0)),
  c = b = b1
  ][c]),
  res = Table.SelectRows(add, each ([primo] = true))
  [[#"Number 1 "],[Number 2]]
in
  res

EnterpriseDNA · May 19, 2023, 11:49am

LinkedIn Post by:
Zoran Milokanović

Twin Prime Numbers w/ #powerquery. #bitanbit #powerbi

let
Source = Excel.CurrentWorkbook(){[Name="Input"]}[Content],
IsPrime = (n) => not List.Accumulate({2..Number.RoundDown(Number.Sqrt(n))}, false, (s, d) => s or (Number.Mod(n, d) = 0)),
Solution = Table.SelectRows(Source, each IsPrime([#"Number 1 "]) and IsPrime([Number 2]) and Number.Abs([#"Number 1 "] - [Number 2]) =2)
in
Solution

EnterpriseDNA · May 19, 2023, 11:49am

LinkedIn post by:
Omid Motamedisedeh

let
  Source = Excel.CurrentWorkbook(){[Name="Table1"]}[Content],
  Prime=(x)=>List.Sum(List.Transform({1..Number.IntegerDivide(x,2)}, each Number.From(Number.Mod(x,_)=0)))=1,
  RESULT=Table.SelectRows(Source, each Prime(_[#"Number 1 "]) and Prime(_[#"Number 2"]) and Number.Abs(_[#"Number 1 "] - _[#"Number 2"])=2)
in
  RESULT

EnterpriseDNA · May 19, 2023, 11:50am

LinkedIn post by:
Brian Julius

I was eager to try Alexis Olson’s cool technique of matching the numbers provided against the Online Encyclopedia of Integer Sequences list of twin primes, but I couldn’t find the link to the list long enough to include all the candidate numbers.

Thus, I fell back on my old standby, the R Primes package called from within Power Query, which makes quick work of this problem…

let
Source = RawData,
FiltAbsDiff2 = Table.SelectRows( Table.AddColumn(Source, "AbsDiff", each Number.Abs( [#"Number1 "] - [Number2]), Int64.Type), each [AbsDiff] = 2),
RunRscript = R.Execute("library(primes)#(lf)df <- dataset#(lf)df$isprime1 <- is_prime(df$Number1)#(lf)df$isprime2 <- is_prime(df$Number2)#(lf)df",[dataset=FiltAbsDiff2]),
RResults = RunRscript{[Name="df"]}[Value],
FilterNonPrimes = Table.SelectRows(RResults, each ([isprime2] = true)),
RemoveOther = Table.SelectColumns(FilterNonPrimes,{"Number1", "Number2"})
in
RemoveOther

EnterpriseDNA · May 19, 2023, 11:55am

LinkedIn Post by:
Stevenson Yu

=LET(A, A2:B10,
B, MAP(TAKE(A,,1), TAKE(A,,-1), LAMBDA(Q,R,
LET(
B, Q,
C, R,
D, ABS(C-B)=2,
E, MIN(MOD(B,SEQUENCE(ROUNDUP(SQRT(B),0)-1,,2)))>0,
F, MIN(MOD(C,SEQUENCE(ROUNDUP(SQRT(C),0)-1,,2)))>0,
G, D*E*F, G))),
FILTER(A, B))

EnterpriseDNA · May 19, 2023, 11:56am

LinkedIn post by:
John Jairo V.

Hi to all!

One option could be:

=FILTER(A2:B10,MAP(A2:A10,B2:B10,LAMBDA(a,b,LET(p,LAMBDA(x,SUM(N(MOD(x,SEQUENCE(x^0.5))=0))),ABS(b-a)=p(b)+p(a)))))

Blessings!

EnterpriseDNA · May 19, 2023, 11:56am

LinkedIn post by:
Bo Rydobon

=FILTER(A2:B10,BYROW(A2:B10,LAMBDA(a,AND(MOD(a,SEQUENCE((MAX(a)^0.5)/2,,3,2)),ABS(SUM(a*{-1,1}))=2))))

EnterpriseDNA · May 19, 2023, 11:57am

LinkedIn Post by:
Sunny Baggu

=LET(
 _list, FILTER(A2:B10, BYROW(A2:B10, LAMBDA(a, ABS(INDEX(a, , 2) - INDEX(a, , 1)) = 2))),
 _num1, DROP(_list, , -1),
 _num2, DROP(_list, , 1),
 FILTER(
 _list,
 MAP(
 _num1,
 _num2,
 SQRT(_num1),
 SQRT(_num2),
 LAMBDA(a, b, c, d,
 LET(
 _r1, OR(MOD(a, SEQUENCE(c - 1, , 2)) = 0),
 _r2, OR(MOD(b, SEQUENCE(d - 1, , 2)) = 0),
 NOT(OR(_r1, _r2))
 )
 )
 )
 )
)

Excel BI Challenge Workout 195

LinkedIn post by Bo Rydobon

LinkedIn Post by: JvdV

LinkedIn Post by: محمد حلمي

LinkedIn post by: Alejandro Simón

LinkedIn post by: Sunny Baggu

LinkedIn post by: Pratik Sathe

LinkedIn Post by: Luan Rodrigues

LinkedIn Post by: Zoran Milokanović

LinkedIn post by: Omid Motamedisedeh

LinkedIn post by: Brian Julius

LinkedIn Post by: Stevenson Yu

LinkedIn post by: Bo Rydobon

LinkedIn Post by: Sunny Baggu